MLP vs KAN on a Real Graph Task

Dataset: Facebook Food Pages | Task: Link Prediction | Models: MLP and KAN

This page shares my MLP results on the same dataset used in my KAN write-up, and then briefly compares the two. For the KAN post, see the full KAN article. See the GitHub repo for code and data: GitHub - SSareen/food-network-analysis-kan.

Results at a Glance

  • Both models perform similarly: ROC-AUC ≈ 0.93, Accuracy/F1 ≈ 0.88.
  • Decision threshold matters: MLP’s best validation threshold ≈ 0.40 (not 0.5); KAN’s best ≈ 0.26.
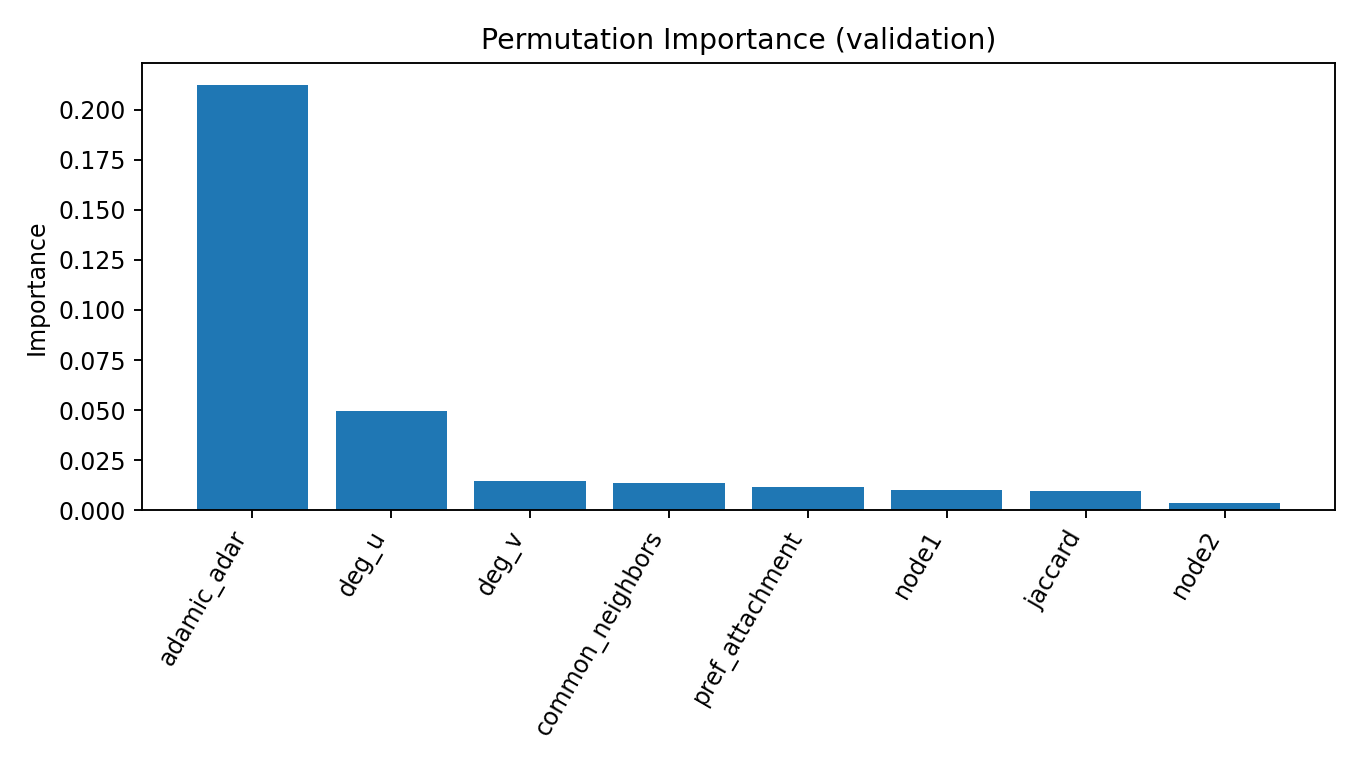
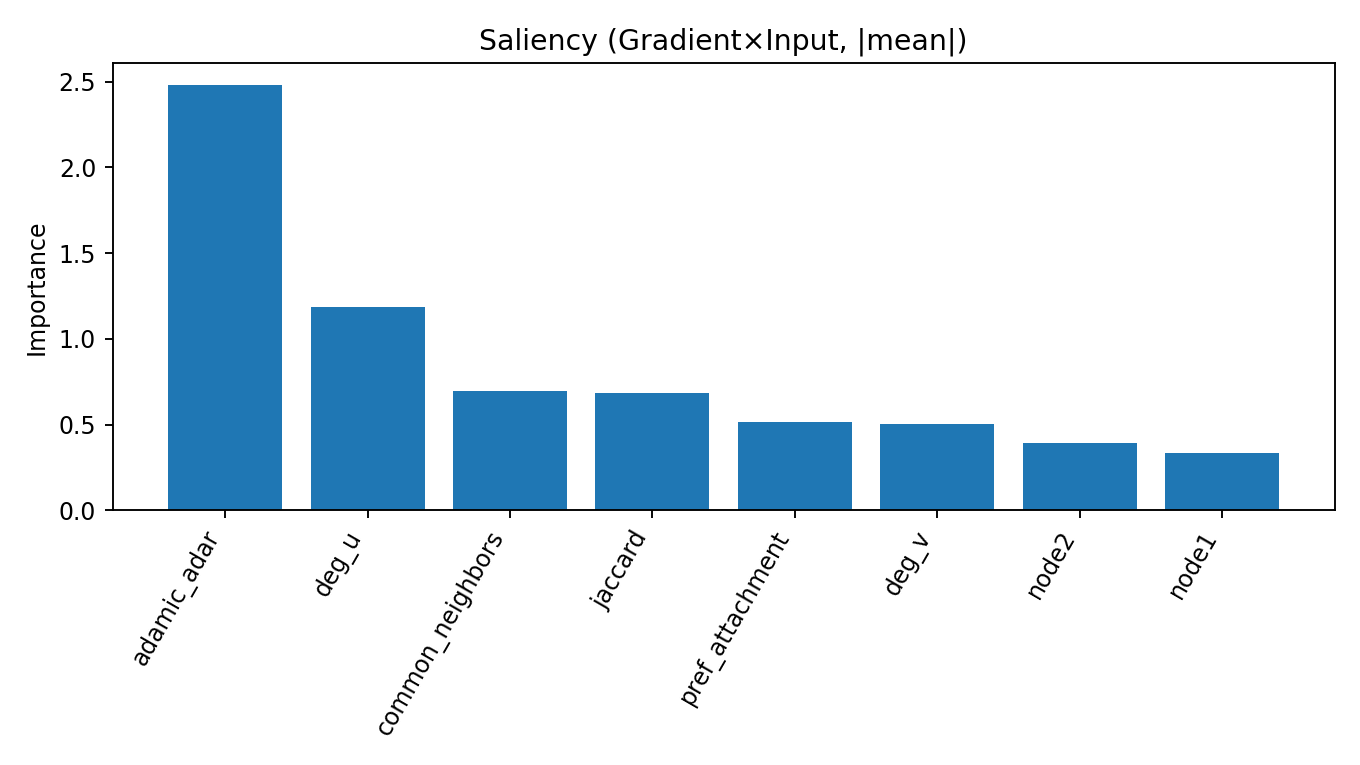
  • Top signal agrees: both rank Adamic-Adar as the most informative feature.
  • Runner-up differs: KAN elevates common_neighbors #2; MLP elevates deg_u #2 (see below sections).
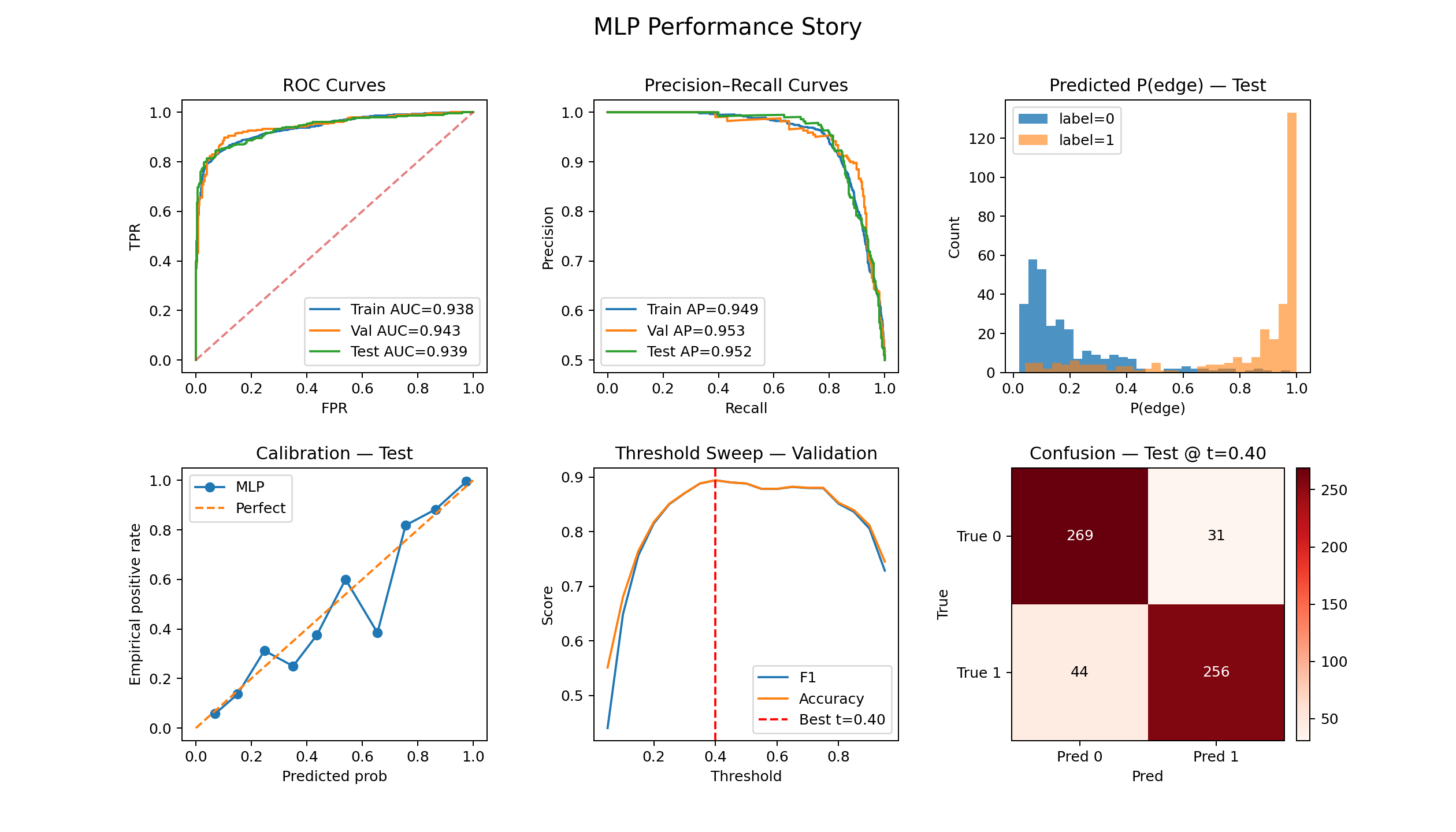
MLP ROC/PR, calibration, threshold sweep, confusion matrix
Fig 1 - MLP Performance Story: stable ROC/PR across splits, near-diagonal calibration, best F1 at t≈0.40.
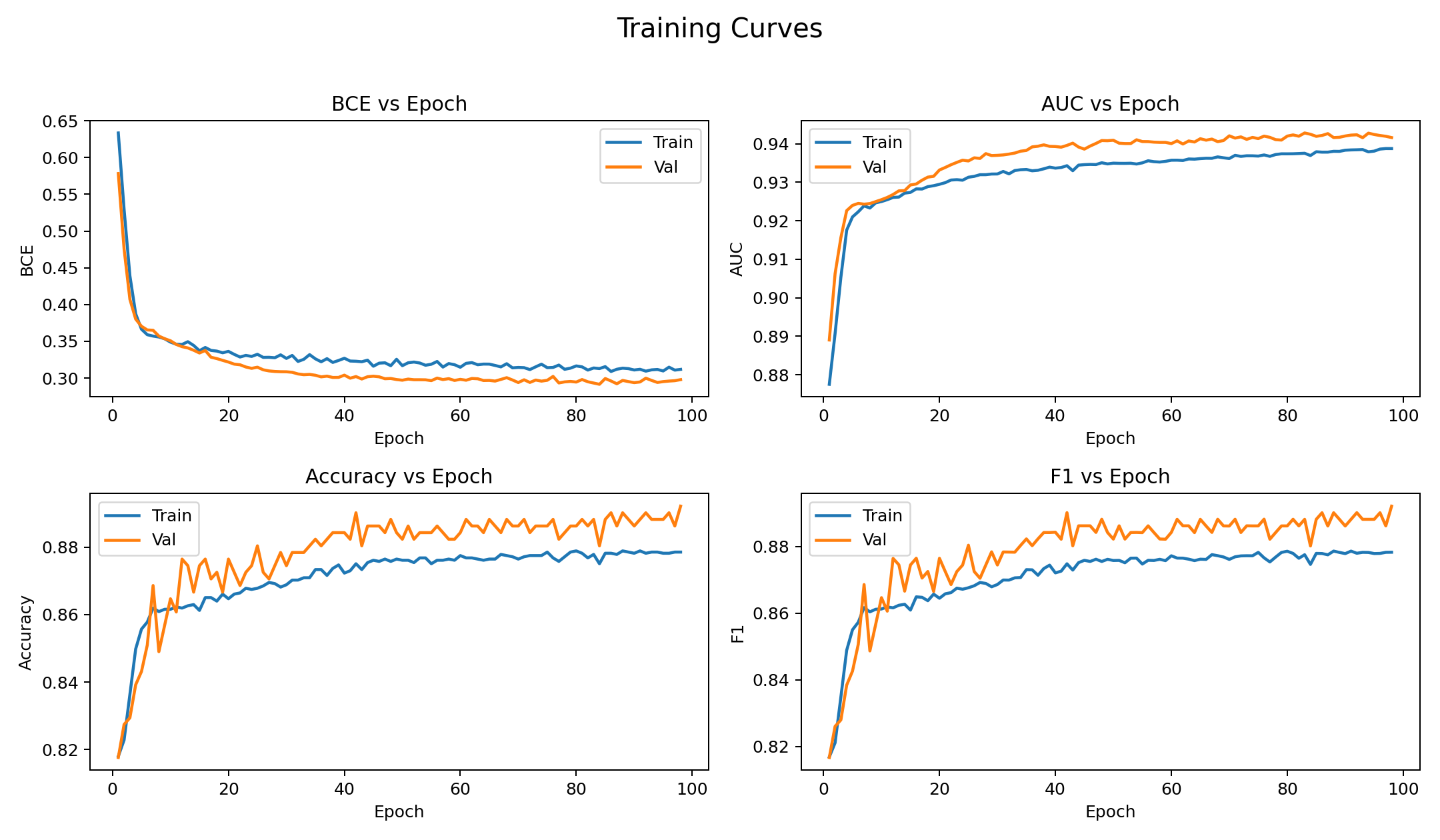
MLP training curves (BCE, AUC, Accuracy, F1)
Fig 2 - Training curves show smooth convergence with train/val tracking closely.
MLP permutation importance
Fig 3 - Permutation importance (global): Adamic-Adar dominates, followed by deg_u.
MLP saliency (|grad×input|)
Fig 4 - Saliency (local sensitivity): same ranking pattern as permutation importance.
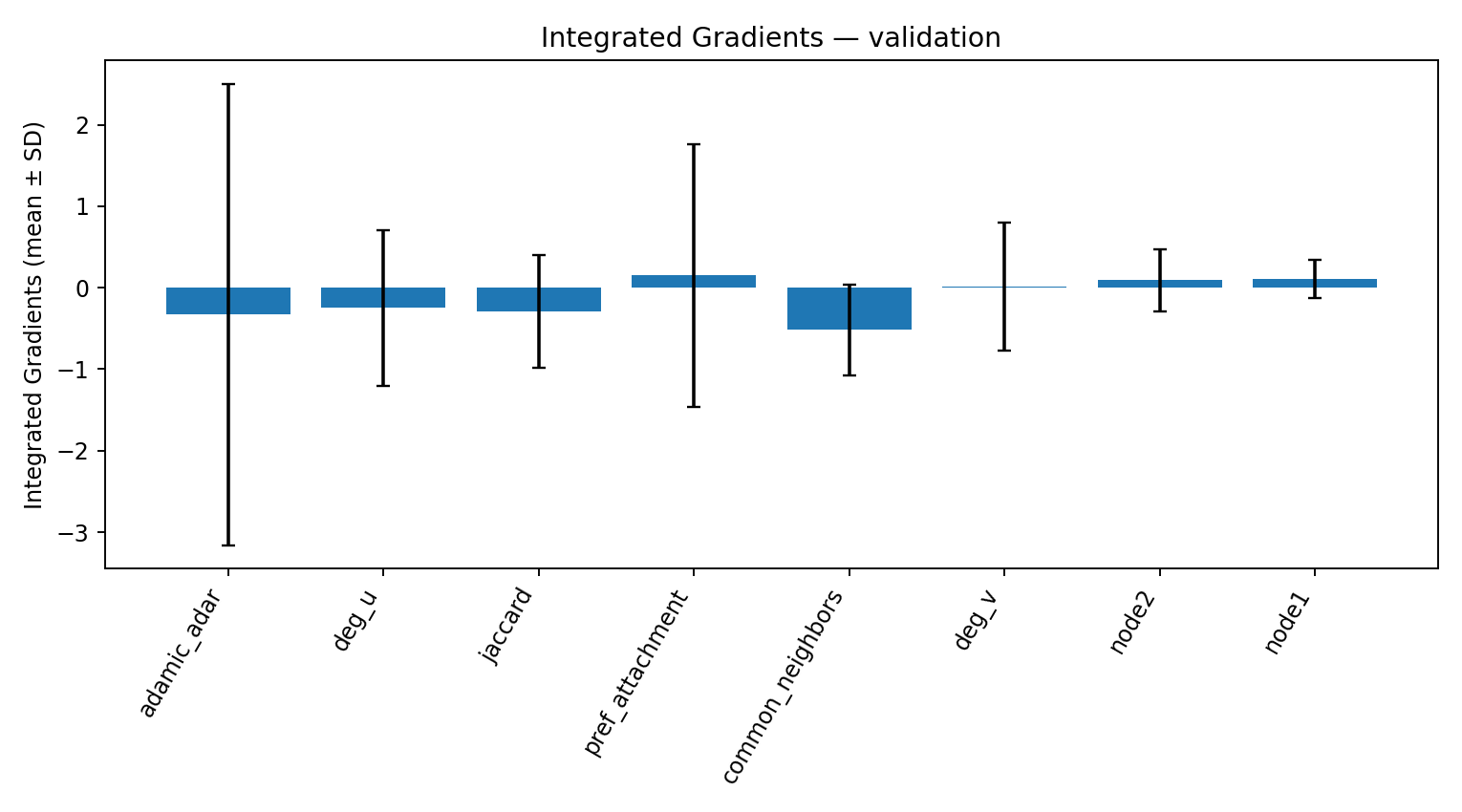
MLP Integrated Gradients (mean±SD)
Fig 5 - Integrated Gradients (signed, mean±SD): wide variance for Adamic-Adar suggests context-dependent effects.

Comparison to KANs

On this dataset, MLP and KAN land in the same performance band. The difference is in how much they tell us about why they work: KAN exposes feature-shape curves (ψ/φ) that show where each feature helps most (including non-monotonic “sweet spots”), while the MLP requires attribution tools to infer that behavior. Both agree that Adamic-Adar is #1; they diverge on #2.

Why KAN ranks Common Neighbors #2 but MLP ranks deg(u) #2

KAN learns a curve for Common Neighbors (CN) directly, so it can decide that “a medium amount of shared neighbors is most useful; very low or very high CN helps less.” MLP doesn’t show that curve explicitly. Instead, it uses the degree of node u as a context knob to judge whether a given CN is meaningful. In other words, the same CN value means different things for a small page vs. a hub, so degree(u) ends up highly useful in the MLP’s attributions.

  • Pair A: CN = 5, deg(u) = 18 (small page) → 5 shared neighbors is strong evidence of a link.
  • Pair B: CN = 5, deg(u) = 800 (hub) → 5 shared neighbors is weak; hubs share neighbors with many pages.

Bottom line: KAN gives more credit to CN because it models the usefulness of CN itself (with a learned shape). The MLP gives more credit to degree(u) because it needs degree to interpret whether a CN count is informative or just hub noise.

KAN ψ/φ: feature shapes and score shaping
Fig 6 - KAN reference (ψ/φ): explicit shape for each feature and the final score mapping.

Glossary

Permutation importance. Shuffle one feature’s values and re-score the model; the drop in a metric (e.g., AUC) estimates that feature’s global usefulness.

Saliency (|grad×input|). Measures how sensitive the prediction is to tiny nudges in a feature around each data point; bigger values mean stronger local influence.

Integrated Gradients. Measures a feature’s contribution by summing the model’s response as that feature goes from a baseline (e.g., zero) to its actual value; larger magnitude = more influence, sign (+/−) = direction.

Dataset citation: 

@inproceedings{nr,
    title={The Network Data Repository with Interactive Graph Analytics and Visualization},
    author={Ryan A. Rossi and Nesreen K. Ahmed},
    booktitle={AAAI},
    url={https://networkrepository.com},
    year={2015}
}