From KAN Theory to Practice - Link Prediction in a Real Network

In my previous blog post, I introduced the Kolmogorov-Arnold Network (KAN) - its structure, why it differs from MLPs, and why its interpretability is worth exploring. Now, let’s make that concrete by solving a real-world graph problem from scratch. Please find the code and data at the bottom of this page.

The Problem - Predicting Links in a Graph

Our dataset is the Facebook Food Pages Network.

  • Nodes - Facebook pages related to food
  • Edges - A “like” from one page to another

The challenge:

Given two pages, can we predict whether there is (or should be) a link between them?

This is the classic link prediction task in network science. It has broad applications - from recommending new friends in social networks, to predicting protein-protein interactions in biology.

Step 1 - Extracting Features

To solve a link prediction problem, we can’t just look at the node IDs - we need structural features that describe how two nodes relate in the network.

I chose six features, all rooted in established measures from graph theory:

  1. Degree of u / Degree of v
    • Number of connections each node has.
    • High-degree nodes (hubs) are more likely to connect with others, but degree alone is rarely decisive.
  2. Common Neighbors
    • How many other nodes both u and v are connected to.
    • Simple but effective - in social graphs, friends of friends are more likely to connect.
  3. Jaccard Coefficient
    • Fraction of shared neighbors relative to total neighbors.
    • Normalizes common neighbors so large hubs don’t dominate.
  4. Adamic-Adar Index
    • Similar to common neighbors, but down-weights “popular” neighbors.
    • Gives more weight to rare, specific shared neighbors - which often signal stronger similarity.
  5. Preferential Attachment Score
    • Product of degrees of u and v.
    • Comes from network growth models where high-degree nodes attract more edges.

Together, these capture local similarity, node popularity, and neighbor specificity - three complementary drivers of link formation in many real networks.

Step 2 - Creating the Dataset

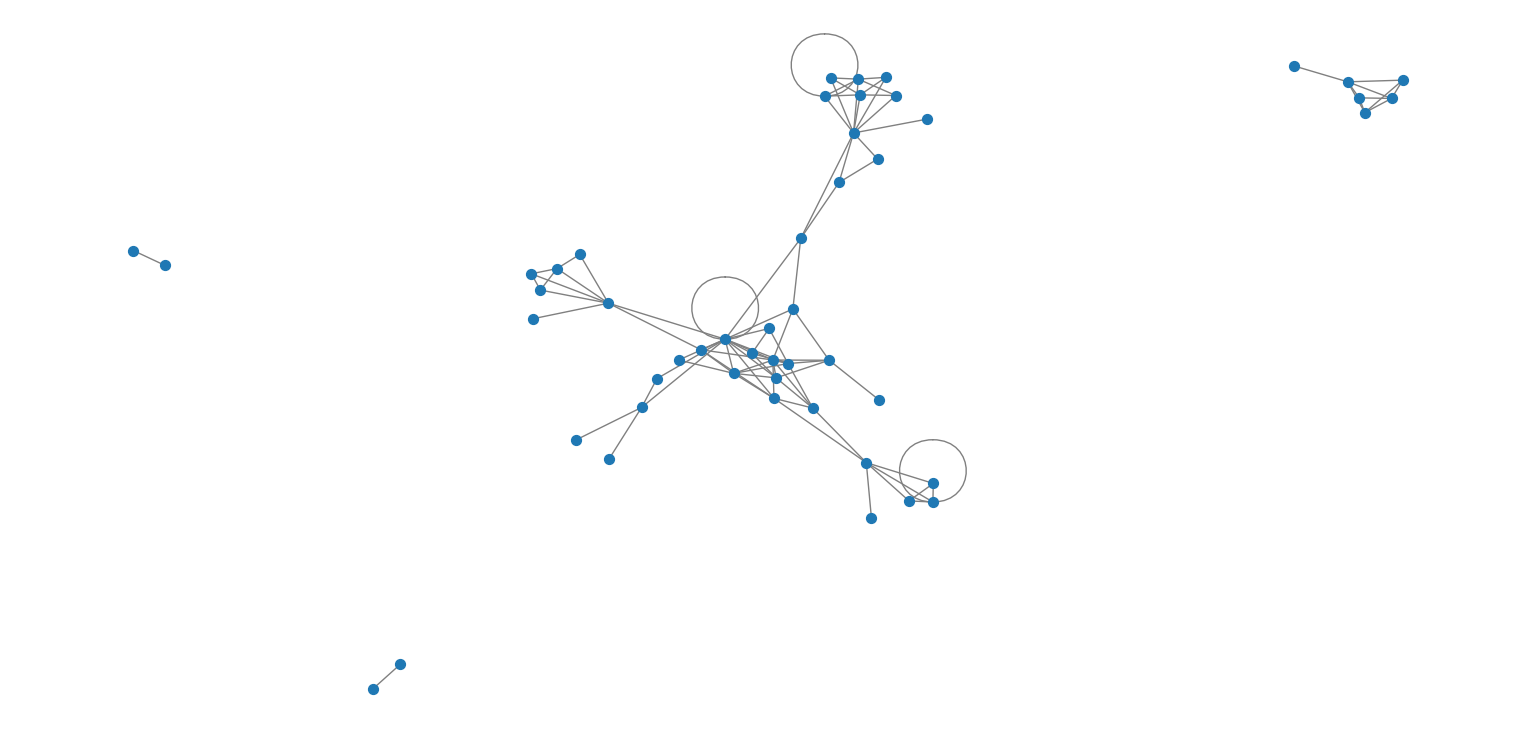
Before computing features, here’s a visual sample from the original Facebook Food Pages Network. Each blue dot represents a page, and edges represent “likes” between them.

Sample of the original Facebook Food Pages Network dataset
Figure X: A sample visualization of the original dataset, showing clusters and connections between Facebook food-related pages.
  1. Load the graph from the .edges file.
  2. Generate positive samples - real edges from the graph.
  3. Generate negative samples - random pairs of unconnected nodes.
  4. Compute the six features for each pair using NetworkX.
  5. Label positives as 1 and negatives as 0.

This gave me a balanced dataset with a total of 4000 pairs of connected and unconnected pairs, ready for training.

Also, to evaluate how informative each feature is, we can visualize the pairwise relationships and distributions of common_neighbors, jaccard, and adamic_adar.

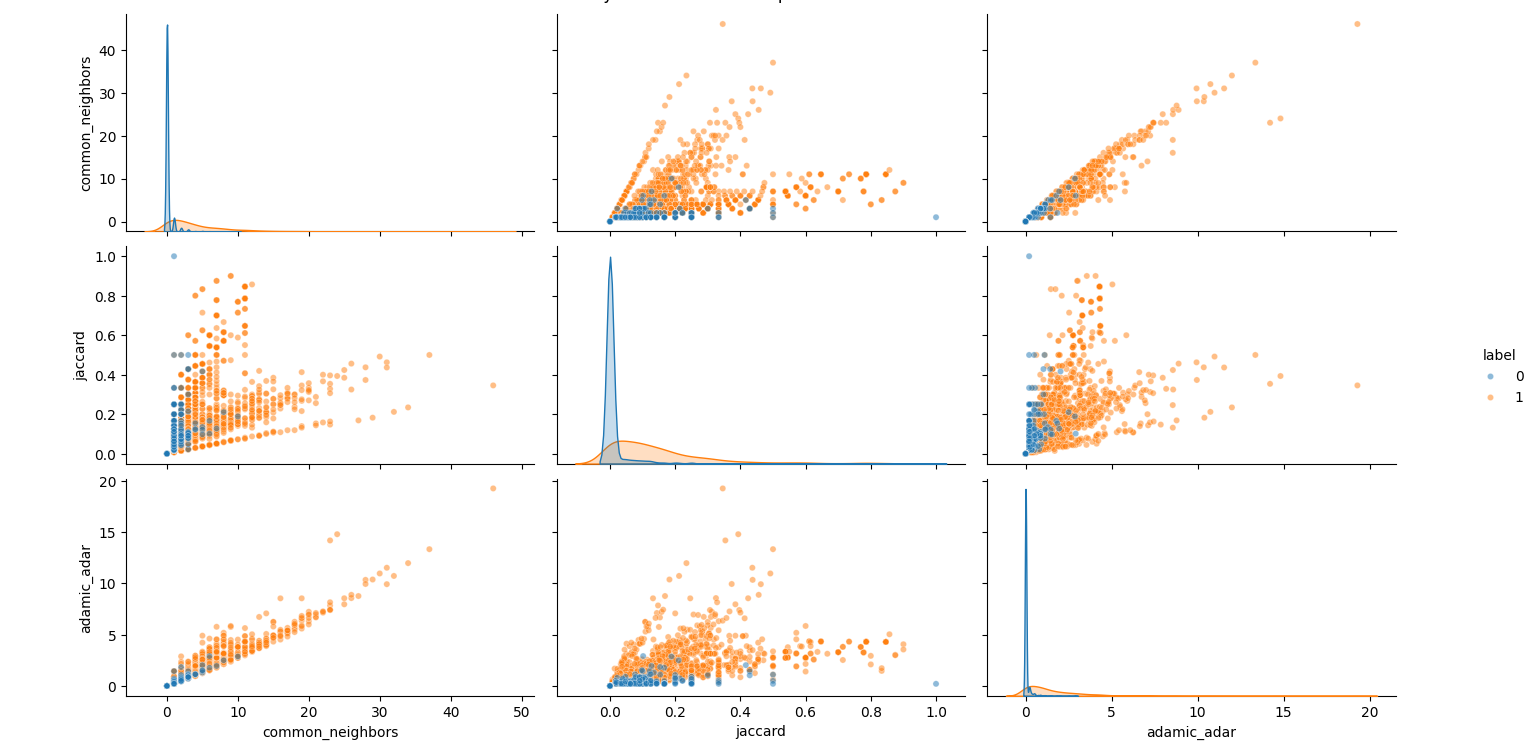
Pairplot of common_neighbors, jaccard, and adamic_adar with label coloring
Figure X: Pairwise relationships between the three main features, with positive (orange) and negative (blue) labels.

All three features have some predictive power - especially common_neighbors and adamic_adar (their orange/blue separation is noticeable). Subtle foreshadowing of the KAN results to come! However, there’s overlap - meaning we’ll still need a classifier to combine them effectively.

Step 3 - Why KAN, and What’s RBF?

A Kolmogorov-Arnold Network differs from an MLP in one key way:

  • Instead of fixed activations (ReLU, tanh), KAN layers use learnable basis functions - often Radial Basis Functions (RBFs).

\[ \phi(x) = e^{-\frac{(x - c)^2}{2\sigma^2}} \]

  • It’s localized - strongest near its center \(c\), weaker farther away.
  • KAN stacks many such functions per feature, letting it model non-linear, non-monotonic relationships without hand-crafting them.

This means:

  • If a feature is useful only in certain ranges (a “sweet spot”), KAN can pick that up naturally.
  • This also makes KAN more interpretable - we can plot exactly how it transforms each feature.

Step 4 - Training the KAN

  • Inputs - the 6 standardized features (mean 0, std 1)
  • Loss - Binary Cross-Entropy
  • Optimizer - Adam (lr=0.003)
  • Epochs - 120, Batch Size - 128

And Why the Parameter Values Make Sense

From my code: Q_TERMS = 6, M_CENTERS = 8, INIT_GAMMA = 1.0. I did not use any tuning beforehand. Instead I used the following logic:

  • Q_TERMS = 6
    Matches the number of input features. This gives each term the capacity to model distinct feature interactions, without redundancy. More terms could lead to overfitting; fewer could miss relationships entirely.
  • M_CENTERS = 8
    Covers the standardized range (-3, 3) evenly, with a center every ~0.75 standard deviations. Enough resolution to capture meaningful bumps and dips without tracking noise.
  • INIT_GAMMA = 1.0
    Starts with moderately broad RBFs so neighboring centers overlap, which ensures smooth gradients and stable early learning. Training can still adapt widths as needed.

Figure 1 - Training Curves

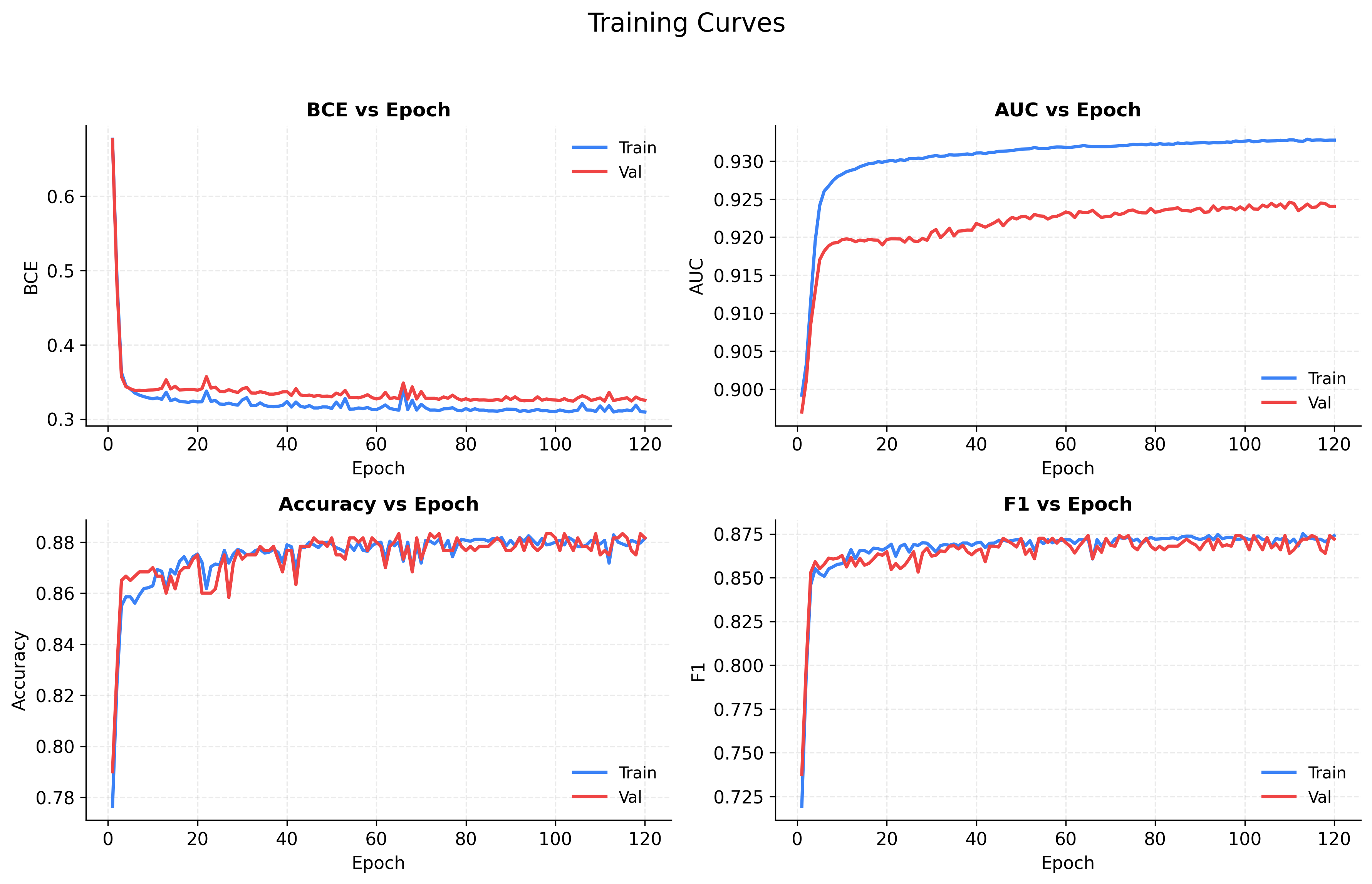
Training curves: BCE loss, accuracy, and F1 vs epochs
Figure 1: The three subplots track the learning process over 120 epochs.
  • Loss (BCE) - Both training and validation loss drop rapidly in the first ~10 epochs and then gradually flatten, showing stable convergence. The curves stay close, indicating no major overfitting.
  • AUC vs. Epoch - Small gap ~0.01 between Train AUC and Validation AUC - which indicates model ranking positive vs. negative pairs very well.
  • Accuracy - Climbs from ~0.78 to ~0.88, plateauing after ~40 epochs. The parallel curves suggest that what the model learns on training data generalizes well.
  • F1 Score - Tracks closely with accuracy, indicating a balanced trade-off between precision and recall - the model isn’t overly favoring one class.

Step 5 - Evaluating Performance

Figure 2 - Performance Story

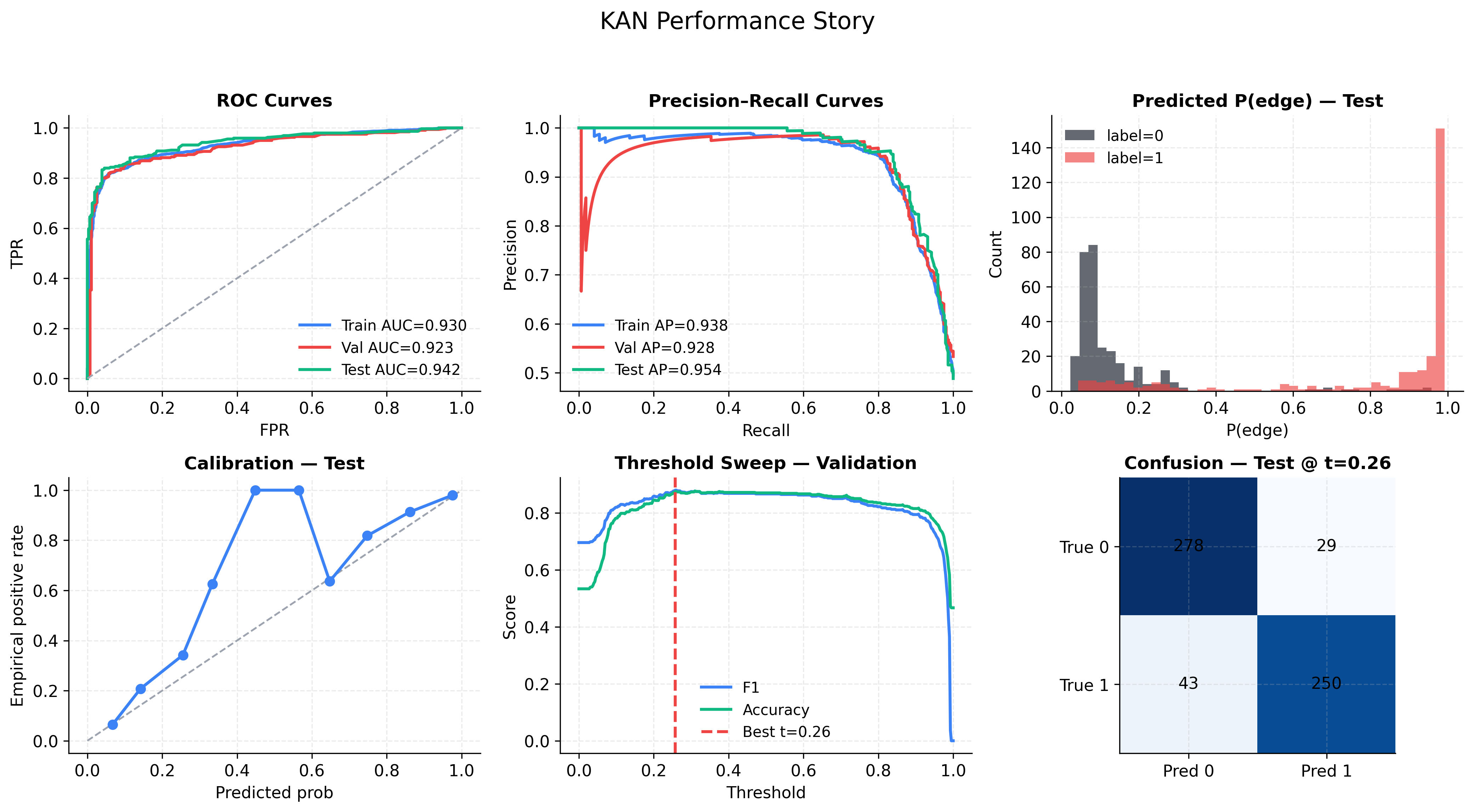
ROC, PR, predicted probability histogram, calibration, threshold sweep, and confusion matrix
Figure 2: This figure evaluates the trained KAN’s decision quality from multiple angles.
  • ROC Curve (top-left) - With AUC ≈ 0.92-0.94 across splits, the model distinguishes linked vs. non-linked pairs with high reliability.
  • Precision-Recall Curve (top-middle) - High average precision (0.93-0.95). At most recall levels, the model keeps precision high. There’s only a dip in precision when recall is extremely high (trying to catch every positive).
  • Probability Histogram (top-right) - Red (true links) cluster near 1.0, black (no links) near 0.0, with only a small overlap - the source of the ~0.88 accuracy ceiling.
  • Calibration Curve (bottom-left) - At predicted probabilities ~0.4–0.6, the actual positive rate spikes higher than expected. Raw probability scores are overconfident in the middle range.
  • Threshold Sweep (bottom-middle) - Best F1 at threshold = 0.26, not 0.5. This shift catches more true positives without flooding with false positives.
  • Confusion Matrix (bottom-right) - Balanced errors (29 FP, 43 FN) against 528 correct predictions. Slightly more missed links than false alarms, but both low.

Step 6 - Understanding What the KAN Learned

Figure 3 - How KAN Learned

ψ transforms for features and φ shaping function for the final score
Figure 3: KANs let us inspect ψ-transforms for each feature and the φ shaping function for the final score.
  • Adamic-Adar (var = 16.84) - Most influential feature. Displays a peak-dip-rise: highest positive influence at slightly below-average values, a penalty just above average, and recovery at very high values - a complex non-linear pattern the model exploits heavily.
  • Common Neighbors (var = 1.23) - Second-most important. The largest boost appears at above-average counts, with a smaller bump for slightly below-average values.
  • Degree of u (var = 0.61) - Minimal influence. Small peaks at low and high extremes, suggesting degree alone is weakly predictive.
  • Shaping Function φ (right) - Maps combined score s_q to link probability. Steep slope near 0 means predictions are highly sensitive in this range - explaining why a 0.26 threshold works better than 0.5. The blue histogram shows most samples lie just above 0, in the “tipping point” zone.

Step 7 - Quick Takeaways

  • Feature engineering - Adamic-Adar and Common Neighbors are the main drivers; Degree is barely used.
  • Non-linear learning - KAN found “sweet spots” where features are most predictive, not just monotonic trends.
  • Interpretability - ψ and φ plots make the model’s reasoning transparent.

Next Step

In a future post, I *might* (no promises) train a standard MLP on the same dataset and compare:

  • Performance metrics
  • How each model uses the same features

Code and Data

Dataset citation: 

@inproceedings{nr,
    title={The Network Data Repository with Interactive Graph Analytics and Visualization},
    author={Ryan A. Rossi and Nesreen K. Ahmed},
    booktitle={AAAI},
    url={https://networkrepository.com},
    year={2015}
}

Code repository: GitHub - SSareen/food-network-analysis-kan